Decision Trees¶
from IPython.display import Image
Image('../../../python_for_probability_statistics_and_machine_learning.jpg')
A decision tree is the easiest classifer to understand, interpret, and explain. A decision tree is constructed by recursively splitting the data set into a sequence of subsets based on if-then questions. The training set consists of pairs $(\mathbf{x},y)$ where $\mathbf{x}\in \mathbb{R}^d$ where $d$ is the number of features available and where $y$ is the corresponding label. The learning method splits the training set into groups based on $\mathbf{x}$ while attempting to keep the assignments in each group as uniform as possible. In order to do this, the learning method must pick a feature and an associated threshold for that feature upon which to divide the data. This is tricky to explain in words, but easy to see with an example. First, let's set up the Scikit-learn classifer,
%matplotlib inline
from matplotlib.pylab import subplots
from numpy import ma
import numpy as np
np.random.seed(12345678)
from sklearn import tree
clf = tree.DecisionTreeClassifier()
Let's also create some example data,
import numpy as np
M=np.fromfunction(lambda i,j:j>=2,(4,4)).astype(int)
print(M)
Programming Tip.
The fromfunction creates Numpy arrays using the indicies as inputs
to a function whose value is the corresponding array entry.
We want to classify the elements of the matrix based on their
respective positions in the matrix. By just looking at the matrix, the
classification is pretty simple --- classify as 0 for any positions in the
first two columns of the matrix, and classify 1 otherwise. Let's walk
through this formally and see if this solution emerges from the decision
tree. The values of the array are the labels for the training set and the
indicies of those values are the elements of $\mathbf{x}$. Specifically, the
training set has $\mathcal{X} = \left\{(i,j)\right\}$ and
$\mathcal{Y}=\left\{0,1\right\}$ Now, let's extract those elements and construct
the training set.
i,j = np.where(M==0)
x=np.vstack([i,j]).T # build nsamp by nfeatures
y = j.reshape(-1,1)*0 # 0 elements
print(x)
print(y)
Thus, the elements of x are the two-dimensional indicies of the
values of y. For example, M[x[0,0],x[0,1]]=y[0,0]. Likewise,
to complete the training set, we just need to stack the rest of the data to
cover
all the cases,
i,j = np.where(M==1)
x=np.vstack([np.vstack([i,j]).T,x ]) # build nsamp x nfeatures
y=np.vstack([j.reshape(-1,1)*0+1,y]) # 1 elements
With all that established, all we have to do is train the classifer,
clf.fit(x,y)
To evaluate how the classifer performed, we can report the score,
clf.score(x,y)
For this classifer, the score is the accuracy, which is defined as the ratio of the sum of the true-positive ($TP$) and true-negatives ($TN$) divided by the sum of all the terms, including the false terms,
$$ \texttt{accuracy}=\frac{TP+TN}{TP+TN+FN+FP} $$In this case, the classifier gets every point correctly, so $FN=FP=0$. On a related note, two other common names from information retrieval theory are recall (a.k.a. sensitivity) and precision (a.k.a. positive predictive value, $TP/(TP+FP)$). We can visualize this tree in Figure. The Gini coefficients (a.k.a. categorical variance) in the figure are a measure of the purity of each so-determined class. This coefficient is defined as,
Example decision tree. The Gini coefficient in each branch
measures the purity of the partition in each node. The samples
item in the box shows the number of items in the corresponding node in the
decision tree.
 $$
\texttt{Gini}_m = \sum_k p_{m,k}(1-p_{m,k})
$$
$$
\texttt{Gini}_m = \sum_k p_{m,k}(1-p_{m,k})
$$where
$$ p_{m,k} = \frac{1}{N_m} \sum_{x_i\in R_m} I(y_i=k) $$which is the proportion of observations labeled $k$ in the $m^{th}$
node and $I(\cdot)$ is the usual indicator function. Note that the maximum value
of
the Gini coefficient is $\max{\texttt{Gini}_{m}}=1-1/m$. For our simple
example, half of the sixteen samples are in category 0 and the other half are
in the 1 category. Using the notation above, the top box corresponds to the
$0^{th}$ node, so $p_{0,0} =1/2 = p_{0,1}$. Then, $\texttt{Gini}_0=0.5$. The
next layer of nodes in Figure is determined by
whether or not the second dimension of the $\mathbf{x}$ data is greater than
1.5. The Gini coefficients for each of these child nodes is zero because
after the prior split, each subsequent category is pure. The value list in
each of the nodes shows the distribution of elements in each category at each
node.
To make this example more interesting, we can contaminate the data slightly,
M[1,0]=1 # put in different class
print(M) # now contaminated
Now we have a 1 entry in the previously
pure first column's second row.
i,j = np.where(M==0)
x=np.vstack([i,j]).T
y = j.reshape(-1,1)*0
i,j = np.where(M==1)
x=np.vstack([np.vstack([i,j]).T,x])
y = np.vstack([j.reshape(-1,1)*0+1,y])
clf.fit(x,y)
The result is shown in Figure. Note the tree has grown significantly due to this one change! The $0^{th}$ node has the following parameters, $p_{0,0} =7/16$ and $p_{0,1}=9/16$. This makes the Gini coefficient for the $0^{th}$ node equal to $\frac{7}{16}\left(1-\frac{7}{16}\right)+\frac{9}{16}(1-\frac{9}{16}) = 0.492$. As before, the root node splits on $X[1] \leq 1.5$. Let's see if we can reconstruct the succeeding layer of nodes manually, as in the following,
y[x[:,1]>1.5] # first node on the right
This obviously has a zero Gini coefficient. Likewise, the node on the left contains the following,
y[x[:,1]<=1.5] # first node on the left
The Gini coefficient in this case is computed as
(1/8)*(1-1/8)+(7/8)*(1-7/8)=0.21875. This node splits based on X[1]<0.5.
The child node to the right derives from the following equivalent logic,
np.logical_and(x[:,1]<=1.5,x[:,1]>0.5)
with corresponding classes,
y[np.logical_and(x[:,1]<=1.5,x[:,1]>0.5)]
Programming Tip.
The logical_and in Numpy provides element-wise logical conjuction. It is not
possible to accomplish this with something like 0.5< x[:,1] <=1.5 because
of the way Python parses this syntax.
Decision tree for contaminated data. Note that just one change in the training data caused the tree to grow five times as large as before!

Notice that for this example as well as for the previous one, the decision tree was exactly able memorize (overfit) the data with perfect accuracy. From our discussion of machine learning theory, this is an indication potential problems in generalization.
The key step in building the decision tree is to come up with the initial split. There are the number of algorithms that can build decision trees based on different criteria, but the general idea is to control the information entropy as the tree is developed. In practical terms, this means that the algorithms attempt to build trees that are not excessively deep. It is well-established that this is a very hard problem to solve completely and there are many approaches to it. This is because the algorithms must make global decisions at each node of the tree using the local data available up to that point.
_=clf.fit(x,y)
fig,axs=subplots(2,2,sharex=True,sharey=True)
ax=axs[0,0]
ax.set_aspect(1)
_=ax.axis((-1,4,-1,4))
ax.invert_yaxis()
# same background all on axes
for ax in axs.flat:
_=ax.plot(ma.masked_array(x[:,1],y==1),ma.masked_array(x[:,0],y==1),'ow',mec='k')
_=ax.plot(ma.masked_array(x[:,1],y==0),ma.masked_array(x[:,0],y==0),'o',color='gray')
lines={'h':[],'v':[]}
nc=0
for i,j,ax in zip(clf.tree_.feature,clf.tree_.threshold,axs.flat):
_=ax.set_title('node %d'%(nc))
nc+=1
if i==0: _=lines['h'].append(j)
elif i==1: _=lines['v'].append(j)
for l in lines['v']: _=ax.vlines(l,-1,4,lw=3)
for l in lines['h']: _=ax.hlines(l,-1,4,lw=3)
The decision tree divides the training set into regions by splitting successively along each dimension until each region is as pure as possible.

For this example, the decision tree partitions the $\mathcal{X}$ space into
different regions corresponding to different $\mathcal{Y}$ labels as shown in
Figure. The root node at the top of
Figure splits the input data based on $X[1] \leq 1.5$.
This
corresponds to the top left panel in Figure (i.e.,
node 0) where the vertical line divides the training data shown into two
regions, corresponding to the two subsequent child nodes. The next split
happens with $X[1] \leq 0.5$ as shown in the next panel of
Figure titled node 1. This continues until the last
panel
on the lower right, where the contaminated element we injected has been
isolated into its own sub-region. Thus, the last panel is a representation of
Figure, where the horizontal/vertical lines
correspond to successive splits in the decision tree.
i,j = np.indices((5,5))
x=np.vstack([i.flatten(),j.flatten()]).T
y=(x[:,0]>=x[:,1]).astype(int).reshape((-1,1))
_=clf.fit(x,y)
fig,ax=subplots()
_=ax.axis((-1,5,-1,5))
ax.set_aspect(1)
ax.invert_yaxis()
_=ax.plot(ma.masked_array(x[:,1],y==1),ma.masked_array(x[:,0],y==1),'ow',mec='k',ms=15)
_=ax.plot(ma.masked_array(x[:,1],y==0),ma.masked_array(x[:,0],y==0),'o',color='gray',ms=15)
for i,j in zip(clf.tree_.feature,clf.tree_.threshold):
if i==1:
_=ax.hlines(j,-1,6,lw=3.)
else:
_=ax.vlines(j,-1,6,lw=3.)
The decision tree fitted to this triangular matrix is very complex, as shown by the number of horizontal and vertical partitions. Thus, even though the pattern in the training data is visually clear, the decision tree cannot automatically uncover it.

Figure shows another example, but now using a simple triangular matrix. As shown by the number of vertical and horizontal partitioning lines, the decision tree that corresponds to this figure is tall and complex. Notice that if we apply a simple rotational transform to the training data, we can obtain Figure, which requires a trivial decision tree to fit. Thus, there may be transformations of the training data that simplify the decision tree, but these are very difficult to derive in general. Nonetheless, this highlights a key weakness of decision trees wherein they may be easy to understand, to train, and to deploy, but may be completely blind to such time-saving and complexity-saving transformations. Indeed, in higher dimensions, it may be impossible to even visualize the potential of such latent transformations. Thus, the advantages of decision trees can be easily outmatched by other methods that we will study later that do have the ability to uncover useful transformations, but which will necessarily be harder to train. Another disadvantage is that because of how decision trees are built, even a single misplaced data point can cause the tree to grow very differently. This is a symptom of high variance.
In all of our examples, the decision tree was able to memorize the training
data exactly, as we discussed earlier, this is a sign of potential
generalization errors. There are pruning algorithms that strategically remove
some of the deepest nodes. but these are not yet fully implemented in
Scikit-learn, as of this writing. Alternatively, restricting the maximum depth
of the decision tree can have a similar effect. The DecisionTreeClassifier
and DecisionTreeRegressor in Scikit-learn both have keyword arguments that
specify maximum depth.
Random Forests¶
It is possible to combine a set of decision trees into a larger
composite tree that has better performance than its individual
components by using ensemble learning. This is implemented in
Scikit-learn as RandomForestClassifier. The composite tree helps
mitigate the primary weakness of decision trees --- high variance.
Random forest classifiers help by averaging out the predictions of
many constituent trees to minimize this variance by randomly selecting
subsets of the training set to train the embedded trees. On the
other hand, this randomization can increase bias because there may be
a subset of the training set that yields an excellent decision tree,
but the averaging effect over randomized training samples washes this
out in the same averaging that reduces the variance. This is a key
trade-off. The following code implements a simple random forest
classifer from our last example.
from numpy import sin, cos, pi
rotation_matrix=np.matrix([[cos(pi/4),-sin(pi/4)],
[sin(pi/4),cos(pi/4)]])
xr=(rotation_matrix*(x.T)).T
xr=np.array(xr)
fig,ax=subplots()
ax.set_aspect(1)
_=ax.axis(xmin=-2,xmax=7,ymin=-4,ymax=4)
_=ax.plot(ma.masked_array(xr[:,1],y==1),ma.masked_array(xr[:,0],y==1),'ow',mec='k',ms=15)
_=ax.plot(ma.masked_array(xr[:,1],y==0),ma.masked_array(xr[:,0],y==0),'o',color='gray',ms=15)
_=clf.fit(xr,y)
for i,j in zip(clf.tree_.feature,clf.tree_.threshold):
if i==1:
_=ax.vlines(j,-1,6,lw=3.)
elif i==0:
_=ax.hlines(j,-1,6,lw=3.)
Using a simple rotation on the training data in [Figure](#fig:example_tree_004), the decision tree can now easily fit the training data with a single partition.

from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import train_test_split, cross_val_score
X_train,X_test,y_train,y_test=train_test_split(x,y,random_state=1)
clf = tree.DecisionTreeClassifier(max_depth=2)
_=clf.fit(X_train,y_train)
rfc = RandomForestClassifier(n_estimators=4,max_depth=2)
_=rfc.fit(X_train,y_train.flat)
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier(n_estimators=4,max_depth=2)
rfc.fit(X_train,y_train.flat)
def draw_board(x,y,clf,ax=None):
if ax is None: fig,ax=subplots()
xm,ymn=x.min(0).T
ax.axis(xmin=xm-1,ymin=ymn-1)
xx,ymx=x.max(0).T
_=ax.axis(xmax=xx+1,ymax=ymx+1)
_=ax.set_aspect(1)
_=ax.invert_yaxis()
_=ax.plot(ma.masked_array(x[:,1],y==1),ma.masked_array(x[:,0],y==1),'ow',mec='k')
_=ax.plot(ma.masked_array(x[:,1],y==0),ma.masked_array(x[:,0],y==0),'o',color='gray')
for i,j in zip(clf.tree_.feature,clf.tree_.threshold):
if i==1:
_=ax.vlines(j,-1,6,lw=3.)
elif i==0:
_=ax.hlines(j,-1,6,lw=3.)
return ax
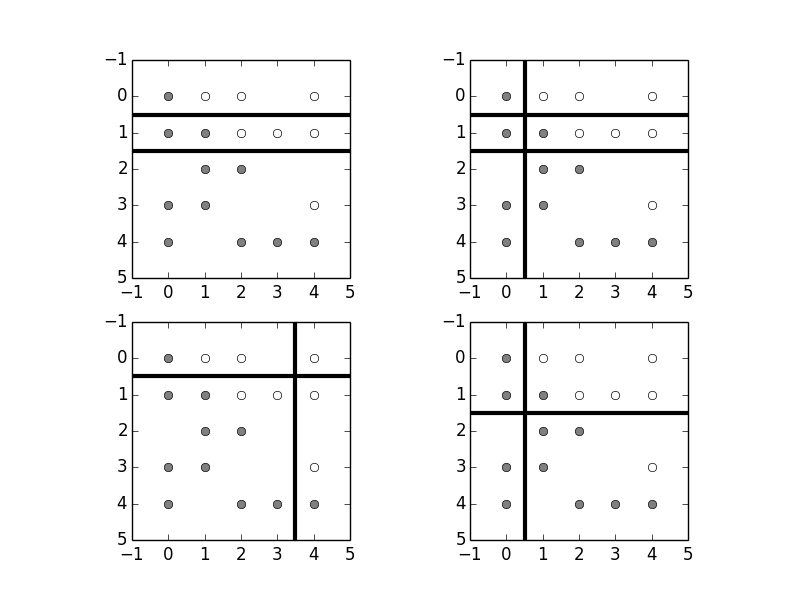
fig,axs = subplots(2,2)
# draw constituent decision trees
for est,ax in zip(rfc.estimators_,axs.flat):
_=draw_board(X_train,y_train,est,ax=ax)
Note that we have constrained the maximum depth max_depth=2 to help
with generalization. To keep things simple we have only set up a forest with
four individual classifers 1. Figure shows
the individual classifers in the forest that have been trained above. Even
though all the constituent decision trees share the same training data, the
random forest algorithm randomly picks feature subsets (with replacement) upon
which to train individual trees. This helps avoid the tendency of decision
trees to become too deep and lopsided, which hurts both performance and
generalization. At the prediction step, the individual outputs of each of the
constituent decision trees are put to a majority vote for the final
classification. To estimate generalization errors without using
cross-validation, the training elements not used for a particular constituent
tree can be used to test that tree and form a collaborative estimate of
generalization errors. This is called the out-of-bag estimate.
to make the figures reproducible in the IPython Notebook corresponding to this section.
The constituent decision trees of the random forest and how they partitioned the training set are shown in these four panels. The random forest classifier uses the individual outputs of each of the constituent trees to produce a collaborative final estimate.
The main advantage of random forest classifiers is that they require very
little tuning and provide a way to trade-off bias and variance via averaging
and randomization. Furthermore, they are fast and easy to train in parallel
(see the n_jobs keyword argument) and fast to predict. On the downside, they
are less interpretable than simple decision trees. There are many other
powerful tree methods in Scikit-learn like ExtraTrees and Gradient Boosted
Regression Trees GradientBoostingRegressor which are discussed in the online
documentation.
We have also set the random seed to a fixed value↩